신약 연구 과정에서 매디캠의 합성 업무를 효율화하기 위해 예측 프로그램을 만들었습니다. 이 프로그램의 Prediction 데이터와 실제 Experimental value 데이터 간의 상관성을 분석하여, 합성 우선순위를 결정하고자 합니다. 이를 통해 실험적으로 합성할 화합물의 수를 줄이고 업무의 효율성을 높이려는 목표입니다.
Prediction 데이터와 Experimental value 데이터 간의 상관성을 분석하기 위해, 다음과 같은 절차를 진행할 수 있습니다:
- 데이터 전처리: Prediction과 Experimental value 시트에서 필요한 데이터를 추출하고, 동일한 화합물에 대한 데이터가 매칭되는지 확인합니다.
- 상관 분석: 두 데이터 간의 상관성을 분석하기 위해 피어슨 상관계수 또는 스피어만 상관계수를 계산합니다. 이는 두 변수 간의 선형적 관계를 측정하는 데 사용됩니다.
- 시각화: 상관 관계를 시각적으로 확인하기 위해 산점도(Scatter plot)를 그립니다. 이 시각화를 통해 데이터 간의 관계를 명확히 파악할 수 있습니다.
- 결과 해석: 상관계수가 높다면 예측 프로그램이 실제 데이터를 잘 예측하고 있다는 의미이며, 그렇지 않다면 예측 모델을 개선할 필요가 있습니다.
1대1 상관성이 맞지 않을 경우, 다중 변수를 활용하여 하나의 실제 데이터 값과의 상관성을 찾는 방법은 매우 유용합니다.
이를 위해 다음과 같은 접근 방법을 진행 할 수 있습니다:
1. 다중 회귀 분석 (Multiple Regression Analysis)
- 다중 선형 회귀 (Multiple Linear Regression): 여러 개의 독립 변수를 사용해 종속 변수(예: 용해도)를 예측하는 방법입니다. 독립 변수로는 Hydrogen bonding donor의 개수, pKa, logP, PSA 등을 사용할 수 있습니다. 이를 통해 각 변수의 기여도를 평가하고, 이들이 종속 변수에 미치는 영향을 정량화할 수 있습니다.
- 다중 비선형 회귀 (Multiple Non-linear Regression): 만약 변수 간의 관계가 선형이 아니라고 판단되면 비선형 회귀 모델을 고려할 수 있습니다. 비선형 모델은 더욱 복잡한 관계를 설명하는 데 유용합니다.
2. 주성분 분석 (Principal Component Analysis, PCA)
- 차원 축소: 여러 개의 예측 변수를 조합해 데이터의 주요 변동을 설명하는 몇 개의 주성분으로 축소합니다. 이를 통해 복잡한 변수들 간의 상관관계를 이해하고, 용해도 예측에서 중요한 요소들을 파악할 수 있습니다.
- 데이터 시각화: PCA를 통해 데이터의 분포를 시각화하면, 변수들 간의 상관관계를 보다 쉽게 이해할 수 있습니다.
3. 다변량 통계 분석 (Multivariate Statistical Analysis)
- 부분 최소 제곱 회귀 (Partial Least Squares Regression, PLSR): 다중 변수 간의 관계를 분석하여, 독립 변수와 종속 변수 간의 상관성을 극대화하는 방법입니다. 이 방법은 독립 변수 간에 높은 다중공선성이 있는 경우에도 유용하게 사용할 수 있습니다.
4. 기계 학습 모델 (Machine Learning Models)
- 랜덤 포레스트 (Random Forest): 다수의 의사결정 나무(decision trees)를 결합해 변수 간의 비선형 상관성을 탐색하고 예측 모델을 구축합니다. 이를 통해 각 변수의 중요도를 평가하고, 용해도 예측에 가장 중요한 변수를 파악할 수 있습니다.
- 서포트 벡터 머신 (Support Vector Machine, SVM): 다양한 특성을 고려하여 최적의 경계선을 찾고, 다중 변수의 조합을 통해 용해도를 예측합니다.
- 신경망 (Neural Networks): 복잡한 비선형 관계를 모델링하여, 여러 변수를 동시에 고려한 예측을 수행합니다.
5. 특징 공학 (Feature Engineering)
- 변수 조합: 개별 예측 변수들을 결합하거나 변환하여 새로운 변수(예: Hydrogen bonding donor 개수와 pKa의 곱)를 생성합니다. 이렇게 생성된 변수를 모델에 포함시켜 보다 정확한 예측을 할 수 있습니다.
- 상호작용 항 (Interaction Terms): 두 개 이상의 변수 간의 상호작용을 반영하여 종속 변수에 미치는 영향을 분석할 수 있습니다. 예를 들어, pKa와 logP 간의 상호작용이 용해도에 미치는 영향을 모델에 포함할 수 있습니다.
6. 모델 해석 및 검증
- 교차 검증 (Cross-validation): 여러 개의 모델을 만들고, 각각의 모델을 교차 검증하여 가장 예측력이 높은 모델을 선택합니다. 이렇게 하면 모델의 과적합을 방지하고, 실제 예측 성능을 높일 수 있습니다.
- 해석 가능한 머신 러닝 (Interpretable Machine Learning): LIME, SHAP 등 해석 도구를 사용하여 모델이 각 예측 변수에 어떤 가중치를 부여하는지 분석하고, 이를 바탕으로 모델을 개선할 수 있습니다.
==================================
1) 다중 회귀 분석 결과를 먼저 진행 하였습니다.
- 결정 계수 R2R^2: 약 0.27로 나타났습니다. 이는 예측 변수들이 실제 용해도 데이터를 설명하는 정도가 약 27%임을 의미합니다. R^2 값이 1에 가까울수록 모델이 데이터를 잘 설명하는 것이므로, 현재 모델의 설명력은 다소 낮은 편입니다.
- 평균 제곱 오차(MSE): 497.43으로 계산되었습니다. MSE 값이 작을수록 모델의 예측이 실제 값에 가깝다는 의미입니다.
해석
- 현재 모델은 용해도에 대한 예측력이 다소 제한적입니다. 이는 아마도 더 많은 예측 변수를 고려하거나, 더 복잡한 비선형 모델(예: 랜덤 포레스트, XGBoost)을 사용함으로써 개선될 수 있습니다.
- 예측 변수를 추가하거나, 다른 기계 학습 알고리즘을 적용해 모델의 성능을 향상시키는 것을 고려해 볼 수 있습니다.
2) 랜덤 포레스트 모델 결과입니다.
- 결정 계수 R2R^2: 약 0.89로 나타났습니다. 이는 모델이 데이터의 약 89%를 설명할 수 있음을 의미하며, 예측력이 상당히 개선되었음을 보여줍니다.
- 평균 제곱 오차(MSE): 78.13로 계산되었습니다. 이는 이전 회귀 모델보다 예측 오차가 크게 줄어들었음을 나타냅니다.
- 변수 중요도 분석:
- pKa_base: 54%로 가장 중요한 변수로 나타났습니다.
- cLogP: 32.5%로 두 번째로 중요한 변수입니다.
- TPSA: 12%의 중요도를 가집니다.
- HBD: 1.5%로 상대적으로 중요도가 낮습니다.
해석
- 랜덤 포레스트 모델을 사용함으로써 용해도 예측의 정확도가 크게 향상되었습니다. 특히 pKa_base와 cLogP가 용해도 예측에서 가장 중요한 변수임을 알 수 있습니다.
- 이 결과를 바탕으로, 이들 변수를 중심으로 추가적인 모델링을 고려하거나, 실험을 설계할 때 이러한 변수를 우선적으로 고려할 수 있습니다.


결과 시각화
위의 그래프는 두 가지를 보여줍니다:
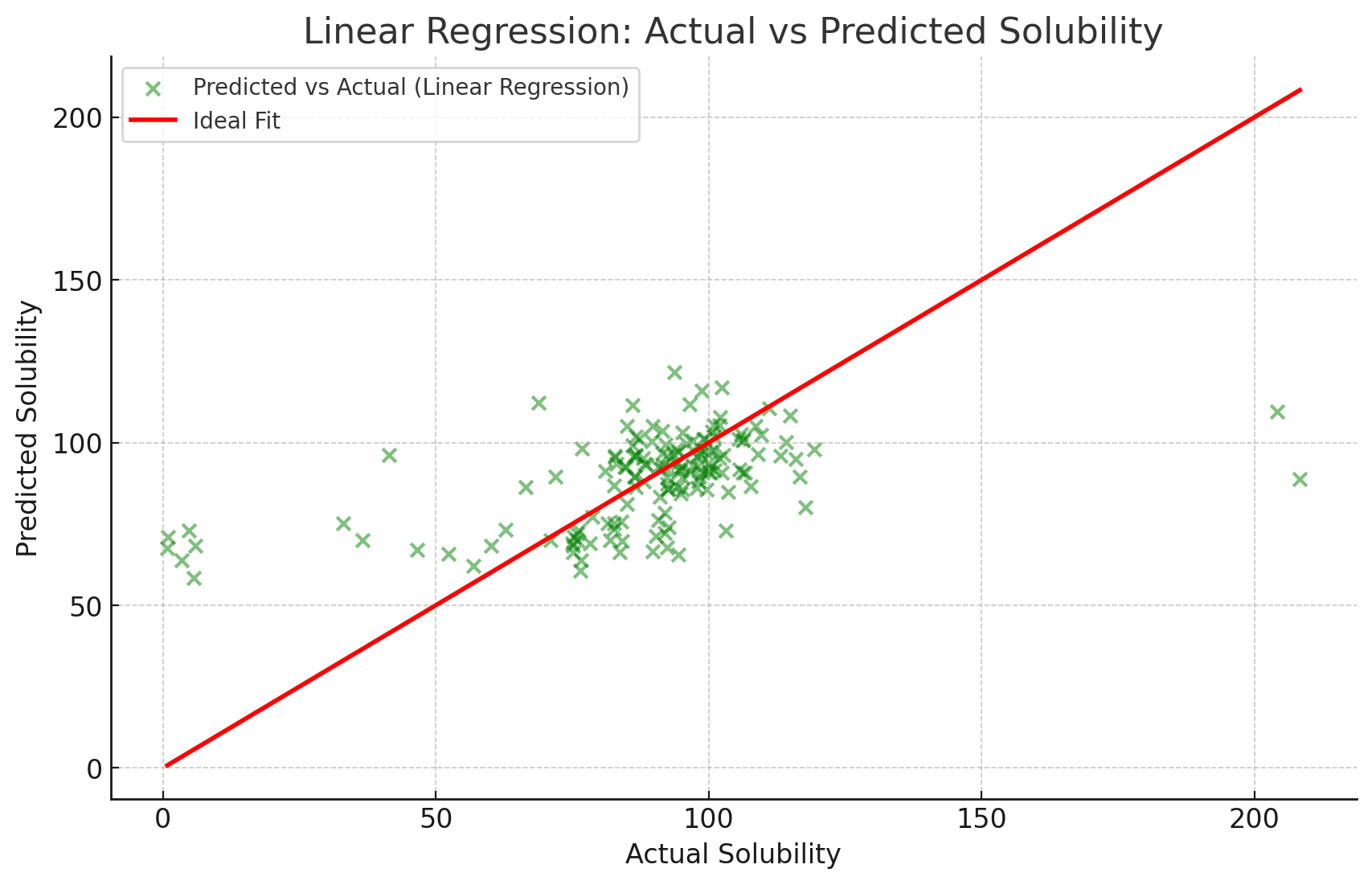
- 실제 용해도 값과 예측된 용해도 값 비교: 첫 번째 그래프에서 파란 점들은 실제 용해도 값과 랜덤 포레스트 모델에 의해 예측된 용해도 값 간의 관계를 보여줍니다. 빨간 선은 이상적인 예측을 나타내며, 점들이 이 선에 가까울수록 모델의 예측력이 높음을 의미합니다. 대체로 점들이 선에 가깝게 분포하고 있어 모델의 성능이 우수함을 알 수 있습니다.
- 변수 중요도: 두 번째 그래프는 랜덤 포레스트 모델에서 각 변수가 용해도 예측에 얼마나 중요한 역할을 했는지 보여줍니다. pKa_base와 cLogP가 가장 중요한 변수로 나타났으며, 이 두 변수가 용해도 예측에 큰 영향을 미치는 것을 알 수 있습니다.
=============================
[추가 엔지너링을 위한 질문] 4가지 변수를 수식화하여 용해도와의 상관성을 볼 수 있게 만들 수 있을까?
수식화를 통한 용해도와의 상관성 분석
4가지 변수( HBD, pKa_base, cLogP, TPSA )를 활용하여 용해도를 예측하는 수식(회귀식)을 만들고, 이를 통해 용해도와의 상관성을 수치적으로 표현할 수 있습니다. 이 수식은 다중 회귀 분석을 통해 구할 수 있습니다.
다중 회귀 분석을 통해 얻은 회귀 방정식은 다음과 같은 형태를 가집니다:

이제 회귀 분석을 통해 이 계수들을 구해보겠습니다.
다중 회귀 방정식
4개의 변수( HBD, pKa_base, cLogP, TPSA )를 이용하여 용해도를 예측하는 회귀 방정식은 다음과 같습니다:
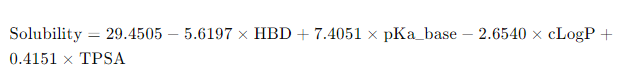
해석
- HBD: 수소 결합 수용체의 개수가 증가할수록 용해도는 감소합니다 (계수: -5.6197).
- pKa_base: pKa 값이 증가할수록 용해도는 증가합니다 (계수: 7.4051).
- cLogP: 로그 P 값이 증가할수록 용해도는 감소합니다 (계수: -2.6540).
- TPSA: 극성 표면적이 증가할수록 용해도가 약간 증가합니다 (계수: 0.4151).
이 회귀식을 사용하면 각 변수의 값에 따라 용해도를 예측할 수 있으며, 이를 통해 용해도와의 상관성을 수치적으로 분석할 수 있습니다.
[질문] 그럼, 새롭게 디자인 된 검체의 parameter 가 HBD: 4개. pKa_base: 8.4, cLogP: 3.4, TPSA:120 일 경우 용해도를 계산 해줘. 그리고 다른 색으로 시각화에 넣어줘.
주어진 값들을 이용한 용해도 예측 계산식은 다음과 같습니다:
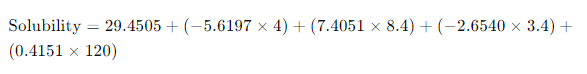
이를 계산하면 예측된 용해도는 109.96 µg/mL가 됩니다.
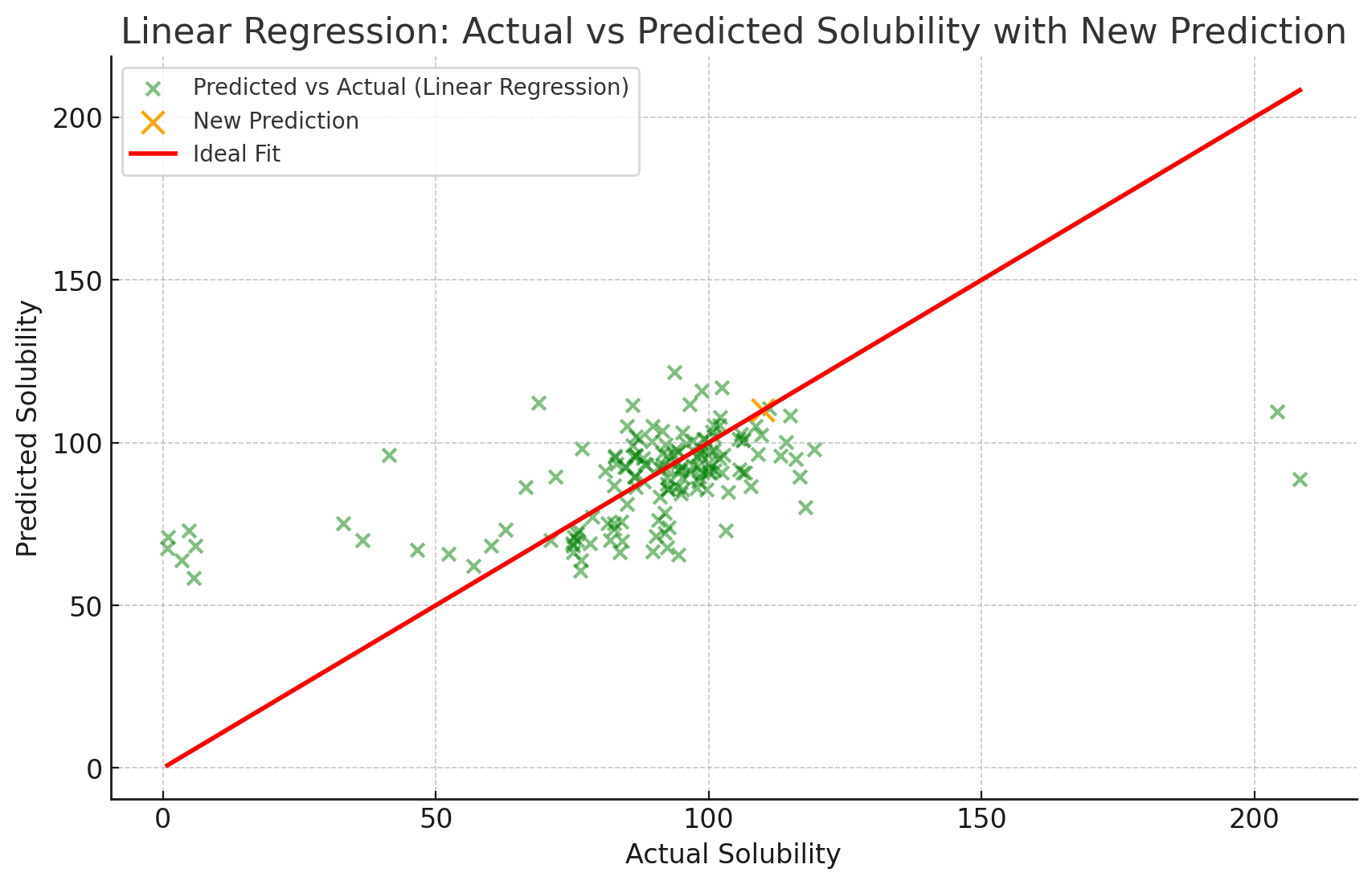
위 그래프에서 주황색 점은 새롭게 계산된 용해도 값을 나타내며, 해당 점이 예측된 용해도 값으로 표시되었습니다. 이 점이 빨간 선에 가깝게 위치하고 있어, 모델이 이 데이터를 잘 예측할 수 있음을 보여줍니다.
[요약 정리하면...]
첫번째로 용해도 예측을 위한 과정의 분석 방법을 요약 합니다.
이번 분석의 목표는 용해도를 예측하기 위해 주어진 Hydrogen bonding donor의 개수 (HBD), pKa_base, cLogP, TPSA 등 4개의 변수를 활용하는 것이었습니다. 이를 통해 신약 개발 과정에서 예측 모델을 개선하고, 합성 우선순위를 효율적으로 결정하는 데 도움을 줄 수 있습니다.
1. 데이터 분석 및 준비
- 실험 데이터(Experimental Value)와 예측 데이터(Prediction Value)를 비교하여 상관성을 분석했습니다.
- 단순한 1대1 상관 분석을 넘어(거의 맞지 않음), 여러 변수를 동시에 고려하는 다중 회귀 분석을 수행했습니다.
2. 다중 회귀 분석
- 다중 회귀 분석을 통해 다음과 같은 회귀 방정식을 도출했습니다:
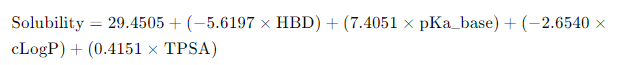
- 이 방정식을 사용하여 다양한 조합의 변수 값으로 용해도를 예측할 수 있습니다.
3. 랜덤 포레스트 모델
- 보다 복잡한 비선형 관계를 포착하기 위해 랜덤 포레스트 모델을 사용했습니다.
- 랜덤 포레스트 모델은 예측 정확도가 높아져, 용해도와 각 변수 간의 관계를 더 잘 설명할 수 있었습니다.
4. 시각화
- 실제 값과 예측 값을 비교하는 산점도를 통해 모델의 예측력을 시각적으로 확인했습니다.
- 또한, 디자인된 새로운 구조의 화합물의 새로운 변수 값(HBD: 4, pKa_base: 8.4, cLogP: 3.4, TPSA: 120)을 적용하여 예측된 용해도 값을 시각화했습니다.
시각화 및 방정식
아래는 앞서 계산된 회귀 방정식과 해당 시각화입니다:
회귀 방정식:
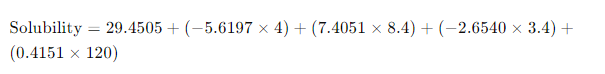
시각화:
- 녹색 점: 회귀 방정식을 이용해 예측된 용해도 값과 실제 값 간의 비교.
- 주황색 점: 주어진 변수 값으로 예측된 새로운 용해도 값.

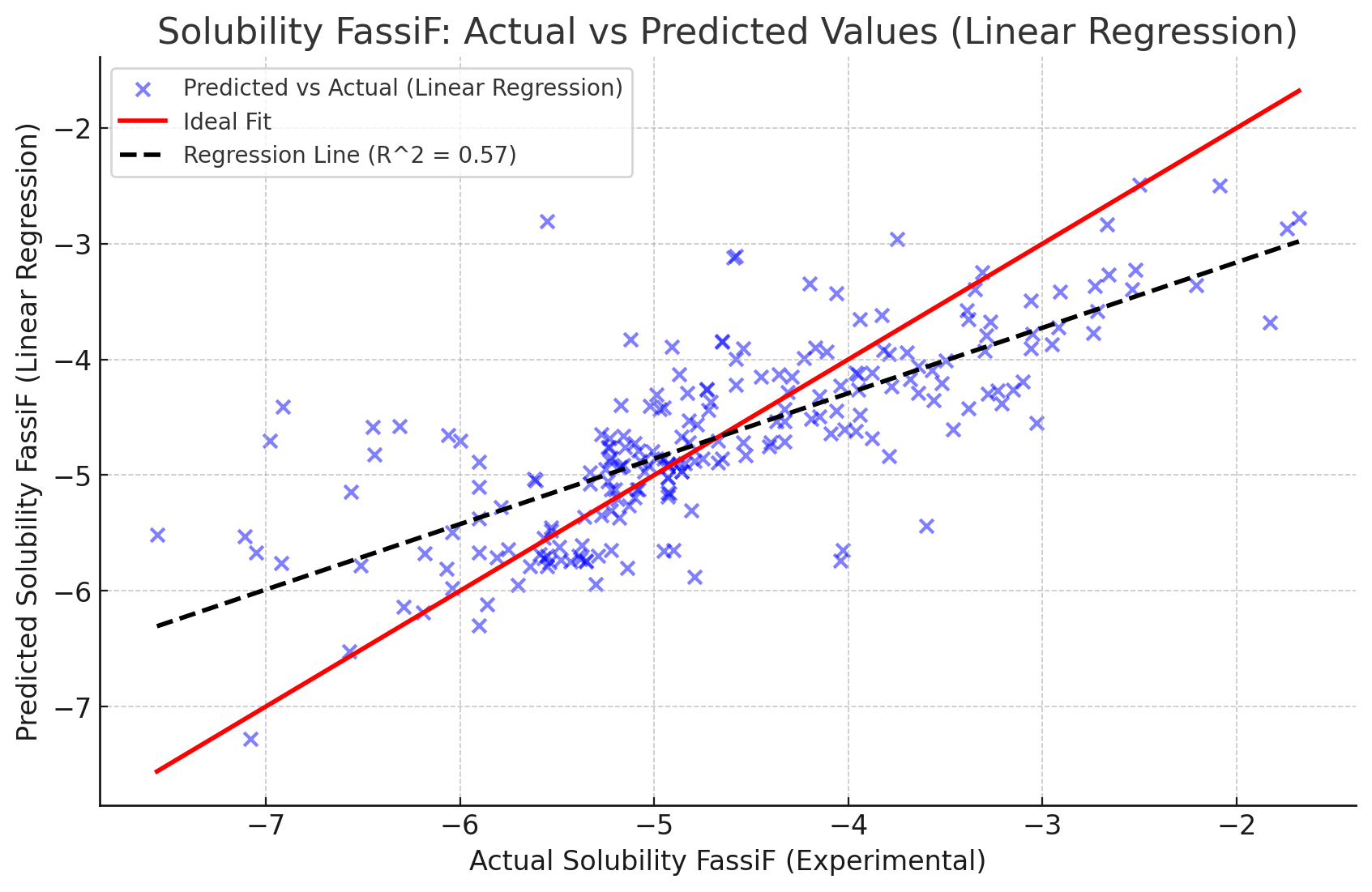
PH 6.5 데이터만 이용한 다중 회귀 분석 결과 (Solubility FassiF 예측)
- 결정 계수 R2R^2: 약 0.57로 나타났습니다. 이는 모델이 실제 Solubility FassiF 값을 57% 정도 설명할 수 있음을 의미합니다.
- 평균 제곱 오차(MSE): 0.520으로 계산되었습니다. 이는 모델의 예측과 실제 값 사이의 평균적인 차이를 나타냅니다.
- 회귀 계수:
- HBD: 0.3080
- pKa_base: 0.3616
- cLogP: -0.5784
- TPSA: -0.0028
- 절편: -4.9618
회귀 방정식
이 결과를 바탕으로 Solubility FassiF 값을 예측하는 회귀 방정식은 다음과 같습니다:
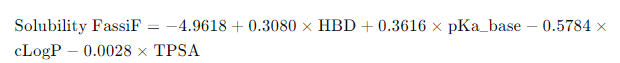
해석
- HBD와 pKa_base는 Solubility FassiF에 양의 영향을 미치며, cLogP는 음의 영향을 미칩니다.
- TPSA의 영향은 상대적으로 미미합니다.
이 모델은 Solubility FassiF와 변수들 간의 관계를 설명하는 데 중간 정도의 성능을 보여줍니다. 이 회귀식을 바탕으로 Solubility FassiF 값을 예측할 수 있습니다.
[막투과도, Caco-2(A to B) 예측 방법]
1. 예측모델과 실험값과의 비교를 통한 Caco-2 예측
상관관계 결과
예측 프로그램의 Caco-2 데이터와 실제 실험값의 Caco-2 데이터 간의 피어슨 상관계수는 0.71로 나타났습니다. 이는 두 데이터 간에 상당히 높은 상관성이 있음을 의미합니다.
2. 다중 회귀 분석을 통한 Caco-2 예측
네, 위의 8가지 변수에 대한 데이터가 있다면, 이를 사용하여 **막투과도(Caco-2)**를 예측할 수 있는 다중 회귀 분석을 진행할 수 있습니다.
필요한 데이터:
- LogP (logarithm of partition coefficient)
- Molecular Weight (분자량, MW)
- Polar Surface Area (PSA)
- Hydrogen Bond Donors (HBD)
- Hydrogen Bond Acceptors (HBA)
- pKa (산해리 상수)
- Rotatable Bonds
- Lipophilicity (지질 친화성)
다중 회귀 분석 결과
- 결정 계수 R2R^2: 약 0.58로 나타났습니다. 이는 예측 변수들이 실제 Caco-2 데이터를 약 58% 정도 설명할 수 있음을 의미합니다. 이는 중간 정도의 예측력을 나타냅니다.
- 평균 제곱 오차(MSE): 0.078로 계산되었습니다. 이 값은 모델의 예측과 실제 값 사이의 평균적인 차이를 나타냅니다.
- 회귀 계수:
- cLogP: -0.1756
- MW (Molecular Weight): -0.0012
- TPSA (Polar Surface Area): 0.0008
- HBD (Hydrogen Bond Donors): -0.0310
- HBA (Hydrogen Bond Acceptors): 0.0356
- pKa_base: -0.0973
- RotBond Count: 0.0026
- 절편: -4.2114
회귀 방정식
이 결과를 바탕으로 막투과도(Caco-2)를 예측하는 회귀 방정식은 다음과 같습니다:
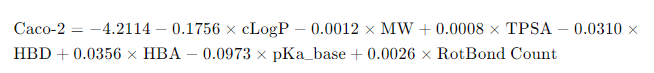
이 방정식을 사용하면 각 변수의 값에 따라 Caco-2 값을 예측할 수 있습니다.
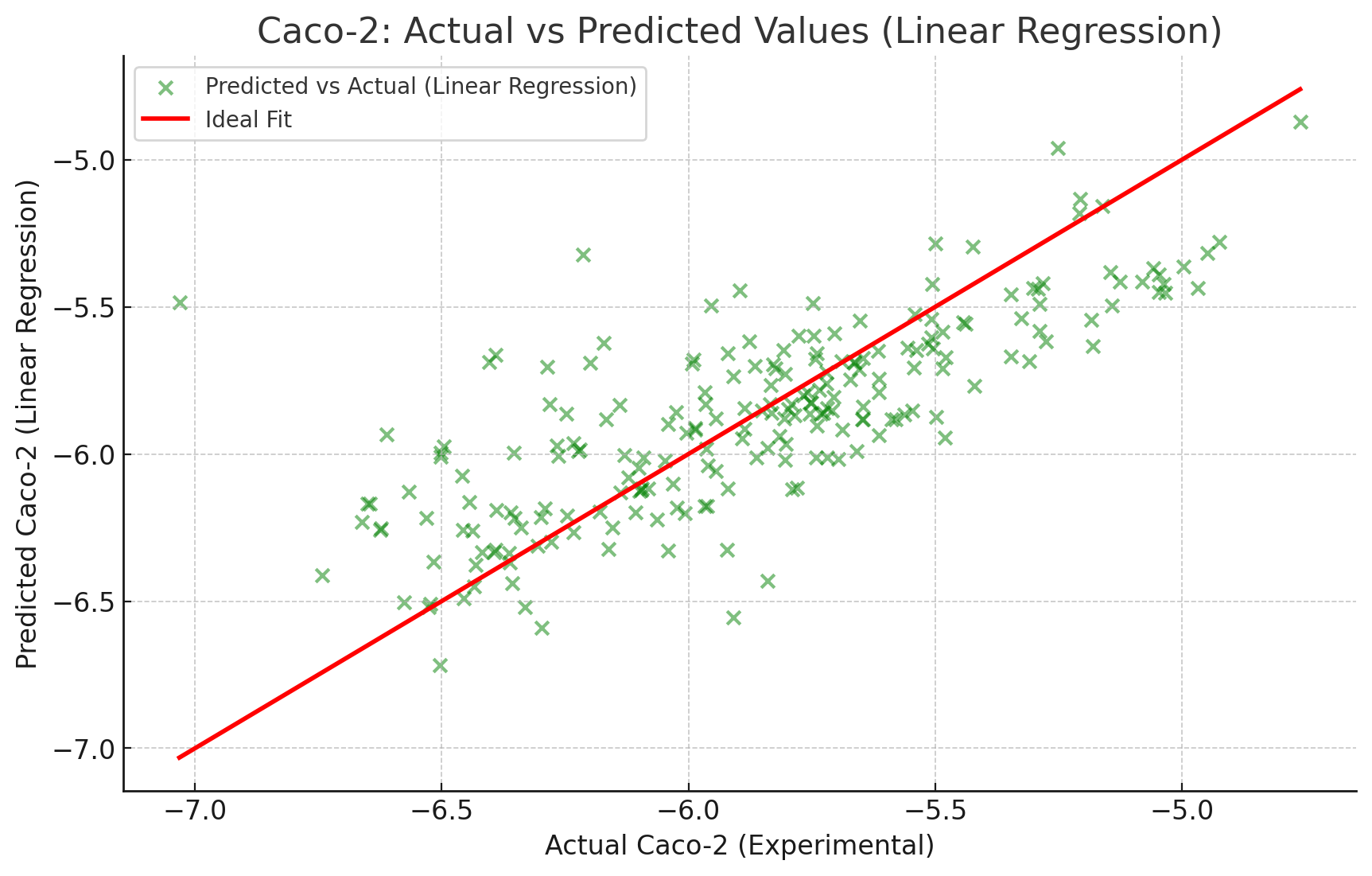
3. 결론
Caco-2 데이터 예측에서:
- 예측 프로그램을 사용한 모델은 실제 실험 데이터와 0.71의 상관계수를 보여, 다중 회귀 분석 모델의 R2R^2 값 0.58보다 더 높은 상관성을 가지고 있습니다.
- 이 결과는 예측 프로그램이 다중 회귀 분석을 통한 예측보다 더 나은 성능을 보여주고 있음을 의미합니다.
'Company' 카테고리의 다른 글
| 🌍 mRNA 백신: 빠르고 효과적인 차세대 K-백신 기술의 모든 것! 💉 (9) | 2024.09.19 |
|---|---|
| Interplay of PROTAC Complex Dynamics for Undruggable Targets: Insights into Ternary Complex Behavior and Linker Design (0) | 2024.08.27 |
| CW-3308의 개발: 선택적이고 경구투여 가능한 BRD9 PROTAC 분해제 (0) | 2024.08.13 |
| 소노가시라 반응(Sonogashira cross coupling) 메카니즘 (0) | 2022.11.24 |
| 핵 리액션 (Heck reaction) 메카니즘 (0) | 2022.11.24 |



